机器数
所谓“机器数”,就是计算机表示的数。我们知道计算机由电路组成,而出于电路的物理特性,只能够表示二进制。大家应该都见过球场的记分板,如果得分就翻动记分板上写着数字的板子使其加 1。我们可以将机器数看成一个长 $n$ 位的记分板,记分板的每一个数位上只有 0 和 1 两种。

由此,我们容易想到三个问题:
- 表示范围不够怎么办?
- 表示不了负数怎么办?
- 表示不了小数怎么办?
对于球场记分来说,3 位十进制数已经够用,且不会有负得分,更不会有小数得分的情况;而计算机不一样,作为用来“计算”的机器,不仅要表示足够大的正整数,还要表示负整数,甚至是小数、复数。因此,我们必须 改变机器数的表示规则,来支持更大范围数的表示。我们给接下来要做的事情起个名字,叫做“编码”。所谓的编码,就是信息从一种形式或格式转换为另一种形式的过程。下面我们要实现的,就是真值(实际的值)与机器数之间的编码。
原码
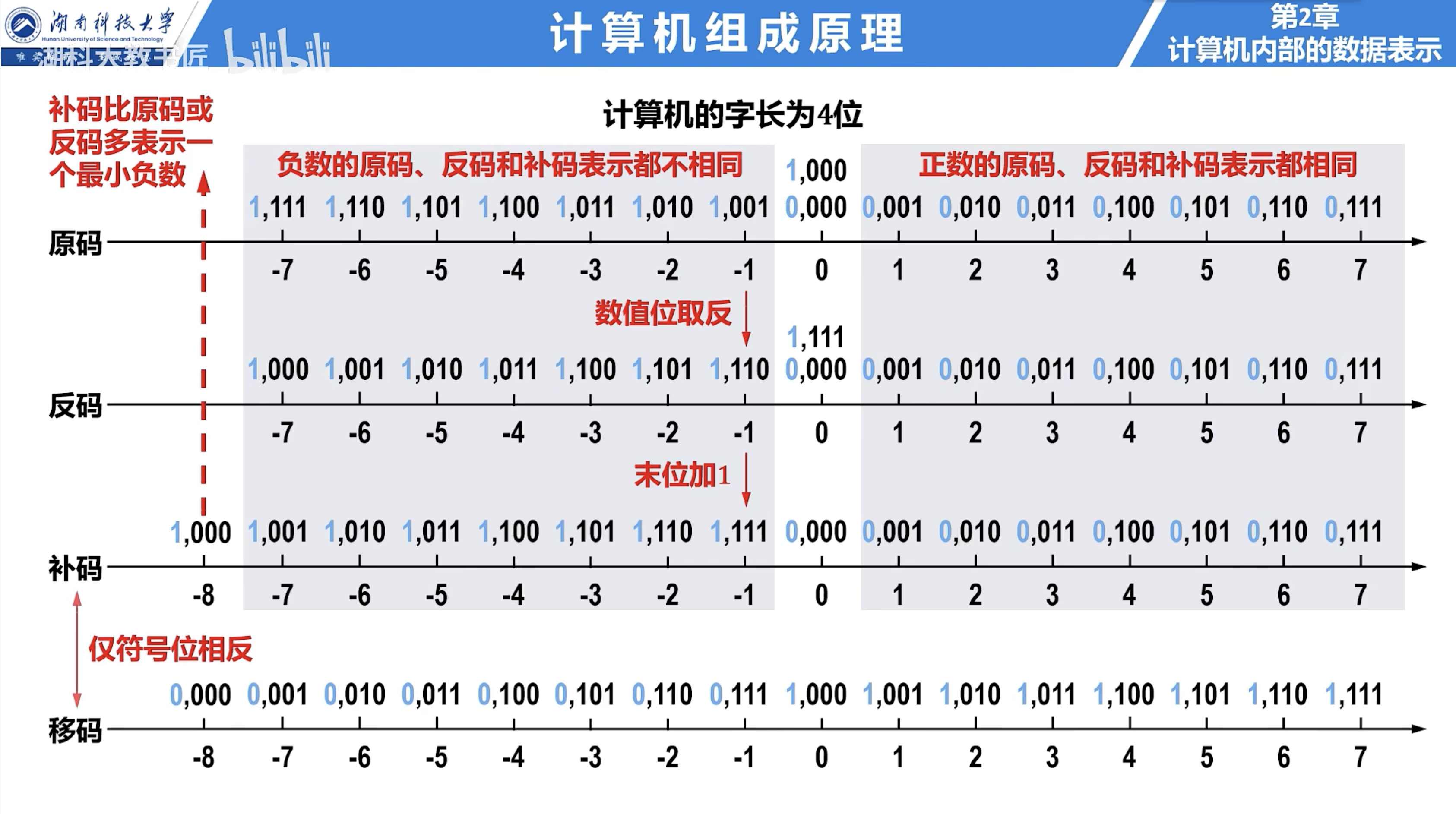
首先,最容易想到的编码方式就是原码,因为它与真值最为相似。我们将最高位拿出来表示符号,0 表示正数,1 表示负数。假设原码有 $n$ 位,那么它就可以实现 $[-(2^n-1), 2^n-1]$ 范围数的表示。
这个范围是关于原点对称的,那么就有一点奇怪:只有当值域长度是奇数时,才会关于原点对称。而我们有 $n$ 位二进制位,理论上可以表示 $2^n$ 种值,而这显然是偶数。为什么少了一个数?这是因为原码中,0 有两种表示:+0 和 -0,即符号位相反,数值位全为 0。这样显而易见的坏处就是浪费了一个对应位置,且 0 的两种表示方式不利于计算。
而原码最致命的缺点在于不便于加减运算。如果两个数都是正数还好说,一旦有负数的参与,运算规则就会变复杂,从而硬件上的设计也会复杂。我们可以尝试按照二进制运算规则直接将一个负数的原码与一个正数的原码相加或相减,是无法得到正确结果的。因此,原码一般只用于浮点数的尾数表示,因为尾数不用考虑符号,只要考虑正数加减即可。
补码
补码是计算机中最常用的一种编码,所有的整数都是补码表示。补码有一个神奇的性质,即“将减法化为加法”。接下来我们就来看下这是怎么实现的。
数论当中有个概念叫做“逆元”。假如有运算 $3\times 7=21$,那么 $21 \times \frac{1}{7}=3$。$\frac{1}{7}$ 取消 了已经发生的乘法运算,我们称 $\frac{1}{7}$ 是 7 的乘法逆元。逆元的概念可以推广到各类计算,例如加法逆元和减法逆元等等。它还可以推广到不同的群(具备二元运算的集合)上。我们接下来要讨论的是在模 $2^n$ 意义下的加法逆元,或者叫(在二进制中的)补数。
上面这段数学概念可能比较晦涩。简单来说,如果我们不方便进行除法运算,那么我们就可以改为乘以除数的乘法逆元;如果我们不方便进行减法运算,那么我们可以改为加上减数的加法逆元。这些运算的结果在它们所在的集合(群)当中是相等的。
简单起见,我们现在只考虑无符号数的机器码。对于 $n$ 位机器数而言,如果结果超过了表示范围,即 $2^n-1$,那么我们只能将存不下的高位丢弃,从数值上来说相当于只留下剩余的“余数”。这不就是取模运算吗,而且模数就是 $2^n$。因此,我们可以将机器数看成“天生带有模 $2^n$ 意义的一个集合”。如果我们想要做减法,只要 加上减数在模 $2^n$ 意义下的加法逆元 就可以了。
那么剩下的问题就是,模意义下的加法逆元怎么求?实际上,对于某个数 $a$,其在模 $2^n$ 意义下的加法逆元 $b$ 的定义是:$a + b \equiv 0 \pmod{2^n}$。意思是,我们找到一个数 $b$,让它与 $a$ 相加的值模上 $2^n$ 等于 0,那么 $b$ 就是要求的那个加法逆元。这个定义也很好理解,如果 $a+b=0$,那么 $b$ 就相当于取消了 $a$ 所进行的加法运算。而我们知道,$0\lt a,b \leq 2^n-1$,那么$0\lt a+b \leq 2^{n+1}-2$。只有当 $a+b=2^n$ 时模的结果才为 0,即 $b = 2^n-a$。有个便于记忆的说法,“补数是对于给定的进位制,相加后能使自然数 $a$ 的位数增加 1 的最小的数。”
我们发现,只有做减法(或加负数)的时候才需要用到补数。因此我们规定,正数的补码等于原码,负数的补码等于符号位加上补数。
反码
反码与其说是一种有用的编码,不如说它是实现原码和补码转换的过渡。它的定义是:正数的反码等于原码,负数的反码除了符号位,其它位全部取反。这相当于只是将原机器数的映射规则翻转了一下,性质完全没有变化,而且表示方式还更不符合人类逻辑了。因此,它不会用于数的表示,但是它对于求 负数 的补码有个方便的性质,那就是:补码 = 反码 + 1。
由于正数的原码、补码、反码全都相同,我们可以不用讨论正数的补码和反码。
我们可以思考一下为什么这个性质成立。首先我们知道补码是原码在模意义下的补数,两者相加自然等于 $2^{n+1}$。而反码就等于原码数值位按位取反,两者相加的数值部份自然是全 1。而全 1 又恰好等于 $2^{n+1}-1$,再加 1 就是 $2^{n+1}$。因此可得补码 = 反码 + 1。
另一种手工计算补码的简便方法被称为扫描法,即从左往右数第一个 1 与其右边的所有 0 不变,剩下的各位(除符号位)取反。这利用了二进制数的特性,没有运算上的意义,因此此处不展开叙述。
移码
让我们脱离基于原码的思路,重新想一下还有什么好用的编码方式。一个简单的思路就是:我们直接用最小的机器数表示值域中最小的真值,然后以此类推。例如,全是 0 的机器数表示真值最小值 $-2^n$,那么全是 1 的机器数表示真值 $2^n-1$。这相当于将机器数表示的“数轴”向左偏移了 $2^n$。我们将这种编码方式叫做移码。
移码最主要的好处就是可以 比较大小,因为它保留了原有的顺序。有个更好的性质:真值的移码和补码仅差一个符号位。比较简单的解释是:补码与移码在数值位的编制方式上完全相同,都是从小到大数值部份依次增加,而移码向左偏移了 $-2^n$,即最高位,自然两者就差一个符号位了。因此,这个性质使移码能够像补码一样进行加减运算。
综上所述,移码最适合作为浮点数阶码的表示,因为我们可以通过阶码的大小来判断两个浮点数的大小,还可以在浮点数运算时计算出结果的阶码。
图片来自 b 站 @湖科大教书匠。
补充
我们讨论了四种常见的机器码编码,并从原理上讲解了每种编码的特点与用途。实际上,这里只主要讲了整数机器数的表示,而对于小数机器数或者说浮点数的表示并没有展开。目前,我们只需要知道浮点数的表示类似科学计数法,用一部份二进制位表示小数点的位置,即阶码;另一部份二进制位表示无小数点的数值,即尾数即可。