前言

我们中的大多数人从未真正学会 KMP 算法。市面上的大多数讲解要么迷失于复杂的记号，要么沉迷公式推导没能抓住本质。本文力争成为最后一篇 KMP 讲解。

需要的知识背景只有字符串的暴力匹配算法，我认为这个算法的难度等价于冒泡排序，因此大一的学生也能够看懂。

概念与记号

• $s[i..i+m-1]$：字符串 $s$ 中从 $s[i]$ 开始，长度为 $m$ 的一个子串。
• 前缀/后缀：字符串 $s$ 中的前/后 $x$ 个字符组成的子串，$0\leq x\leq n$，其中 $n$ 表示 $s$ 的长度。特别的，$x\neq n$ 时的前/后缀称为真前缀/真后缀。由于与原串相等的前缀在字符串匹配问题中没有讨论价值，所以下文中的前后缀均指真前后缀。
• 文本串与模式串：假如我们需要字符串 $s$ 中搜索 $p$，那么 $s$ 是文本串，$p$ 是模式串。

正文

在文本串中匹配模式串

首先，我们回顾 KMP 要解决的字符串匹配问题。

在文本串 $s$ 中找出模式串 $p$ 出现的所有位置。

令 $n$ 表示 $s$ 的长度，$m$ 表示 $p$ 的长度。容易想到 $O(nm)$¹ 的暴力做法，对 $s$ 的每一个位置 $i$，检查 $s[i..i+m-1]$ 是否等于 $p$。我们将这个过程称为一次 匹配。该算法的缺陷在于每次匹配都要回到 $p$ 的开头重新开始（称为 回退），这是不必要的。回退 的目的是重新尝试 $p$ 是否等于 $s$ 的下个子串，如果 $p$ 中有重复的部份，我们就可以将其利用以减少计算。

假设对当前位置 $i$，$s$ 的某个子串已经与 $p$ 的某个长度为 $x$ 的前缀匹配，下一个字符失配。那么就需要回退了。接下来考虑已经匹配的前缀 $t$，假如我们找到 $t$ 的 最长公共前后缀，长度为 $y$。由于 $s$ 的某个子串已经与 $t$ 匹配，即相等，那么回退到最长公共前缀结束的位置即可。

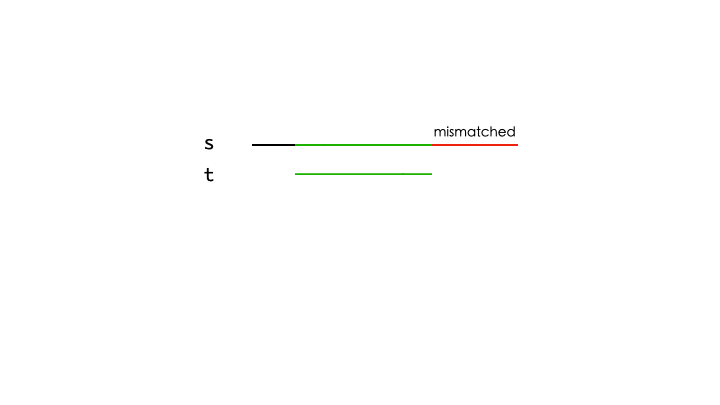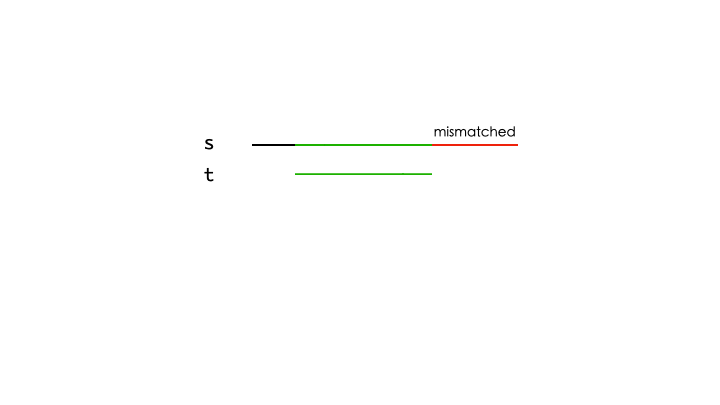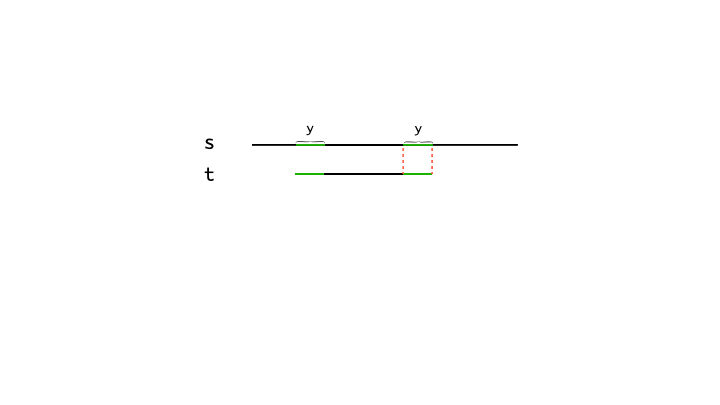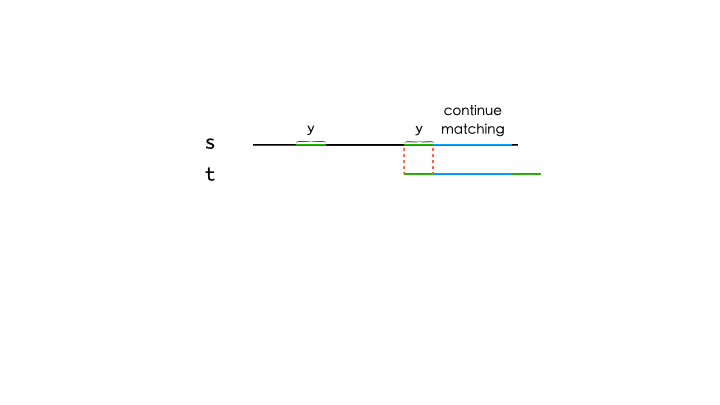
假如我们对模式串 $p$ 的每一个前缀都求出 最长公共前后缀，那么每次失配的时候，我们都可以回退到 最近 的可匹配位置。由于我们求的是 最长 的公共前后缀，那么它与 $s$ 匹配的长度最长，回退的距离也就越短。令所有前缀 $p[0..x]$ 的 最长公共前后缀 长度为 $\textit{next}[x]$。令 $i$ 和 $j$ 表示 $s$ 和 $p$ 当前匹配的位置，$s$ 与 $p$ 的匹配过程如下：

1. 如果 $s[i]$ 与 $p[j]$ 失配，那么 $j\leftarrow \textit{next}[j-1]$² 表示回退。重复这个过程，直到 $s[i]$ 与 $p[j]$ 匹配或者 $j$ 已经回退到开头。
2. 如果 $s[i]$ 与 $p[j]$ 匹配，$j\leftarrow j+1$ 表示匹配长度加 1。
3. 如果 $j$ 已到达末尾，则已发现了 $p$ 的一次匹配。

for (int i = 0, j = 0; i < n; i++) {
    while (j && s[i] != p[j])j = nxt[j - 1];
    if (s[i] == p[j])j++;
    if (j == m)cout << i + 1 - m << endl;
}

求解 $\textit{next}$ 数组

剩下的问题是：我们该如何求解 $p$ 的所有前缀 $p[0..x]$ 的 最长公共前后缀 的长度？其实，这个问题就等价于：

在 $p$ 的后缀中匹配前缀。

那么，这个问题就跟上面我们解决的在文本串中匹配模式串问题是一样的了。在实现中，我们常常写成将 $p$ 错开一位与自身匹配，其实这就是用一个前缀去匹配后缀。

for (int i = 1, j = 0; i < m; i++) {
    while (j && p[i] != p[j]) j = nxt[j - 1];
    if (p[i] == p[j]) j++;
    nxt[i] = j;
}

剩余的问题

等等，感觉有点怪？感觉 KMP 就像左脚踩右脚上天一样，对模式串和文本串进行一样的匹配操作，时间复杂度莫名其妙的就降低了？按照经验，这种类似递归的——自己调用自己的过程——应该不断缩小问题的范围。但匹配文本串和匹配模式串的问题范围应该是一样的，怎么就能得到 $\textit{next}$ 数组？这是因为 $\textit{next}$ 数组是递推得到的。

首先考虑暴力求解 $p$ 的所有前缀 $p[0..x]$ 的 最长公共前后缀 长度，即对于每一个前缀，判断它的每一个前后缀是否相同，时间复杂度 $O(n^3)$。注意到，随着长度增加，最长公共前后缀的长度是单调增加的，那么可以二分这个长度，时间复杂度 $O(n^2\log n)$。进一步，$\textit{next}[i]$ 的值最多是 $\textit{next}[i-1]+1$，不用二分了，时间复杂度 $O(n^2)$。目前的瓶颈在于每次匹配前后缀时都回退到开头。KMP 算法中，由于发生失配时，我们会不断回退直到下一个字符匹配，所以不用进行字符串比较，而是比较两个字符即可，从而时间复杂度 $O(n)$。

后话

KMP 之所以复杂，是因为它糅合了各种算法的思想。比如失配时的回退 while (j && s[i] != p[j])j = next[j - 1]，可以看到动态规划的影子，都是保存状态加速计算的思想，而重复跳转也有并查集的意味。又比如求 next 数组时，注意到前后缀匹配的问题与要解决的字符串匹配问题的等价。另外，对于字符串记号的复杂、模糊，也是增加理解难度的原因之一。还有臭名昭著的“差一问题”，下标从 0 和 1 开始的区别永远也搞不清，代码中一会 +1 一会 -1 仿佛魔法。

很多题解讲解 KMP 时，一开始能够把握住字符串匹配的思路，但后面讲怎么求 next 数组就飘了。也有的题解作纯粹的公式推导，最后得出结论。在我看来这就如同用代数运算去解释函数，无法把握本质。事实上，只要我们把握住 next 数组定义与解题思路，就不会走偏。这也引出了我近来思考的结论——对于个人学习来说，理解 > 公式 > 形式。